It is human nature to want to measure things, or at least calibrate big things against other big things. The big and destructive fairly beg quantifying, in fact, so for instance we have the Saffir-Simpson hurricane wind scale (with a top level of 5 for winds above 156 mph/250 kph). This depends only on wind velocities, and does not take into account either rain or storm surges (Allaby, 2008). We also have the Fujita tornado intensity scale (Fujita, 1971), which for winds above 261 mph/420 kph can reach a level of F5. The following question asks about measuring earthquakes and volcanoes, which are much harder to quantify than wind-speed velocities.
Q: Hi I am an 8th grade student and I was wondering what determines the magnitude of an earthquake or what determines the power of a volcano…
– Caleb Le M.
A: Your question has two parts, which I will answer in order:
- Earthquake magnitudes are calculated many different ways, but ultimately it comes down to measuring the amplitude of the actual ground motion (up-down, side-to-side) on multiple seismometers, and correcting for the varying seismic rock-velocities and the distance separating the seismometers from the earthquake epicenter. Of course, you have to calculate the distance to the epicenter first by triangulation from three or more seismometers (and also correct THOSE results by different seismic velocities in the different rocks between the hypocenter and the different measuring seismometers).
Asking a seismologist how big an earthquake was is like asking a friend to describe how big someone is? Do you mean tall? Wide? Heavy? Some combination of all of these? Does this dress make me look fat? Seismologists do NOT like being asked how they calculate a magnitude, because it will generally require a 30-minute explanation. Therefore, their first reply is often which magnitude are we talking about here?
The original earthquake magnitude scale (Richter, 1935) was the first coherent attempt to define something that is ultimately three-dimensional and very complex. The original Richter scale measured only the energy in the low-frequency end of the seismic energy spectrum, standardized to the particular type of Wood-Anderson seismometer available at the time. Today a modified Richter magnitude is called the “local magnitude” or ML, and is tuned for the rocks and sediments of a local region. For southern California, the equation to calculate this magnitude (Spence et al., 1989; Bormann and Dewey, 2014) is:
ML = Log (A) + 0.00189*r – 2.09,
…where A = amplitude of maximum ground movement in nanometers measured at the seismometer, r = distance from the seismometer to the epicenter in kilometers, and – 2.09 is a correction factor. This equation works only for southern California, and doesn’t work for Cascadia, Japan, the Mediterranean, or Indonesia, which are each served better by different numerical factors. The equation is very simple; if you know the reported magnitude, you can use your smart phone to calculate exactly how much the ground moved under you.
Another way to calculate an earthquake local magnitude is to work off of an analog log-scale diagram such as in this:
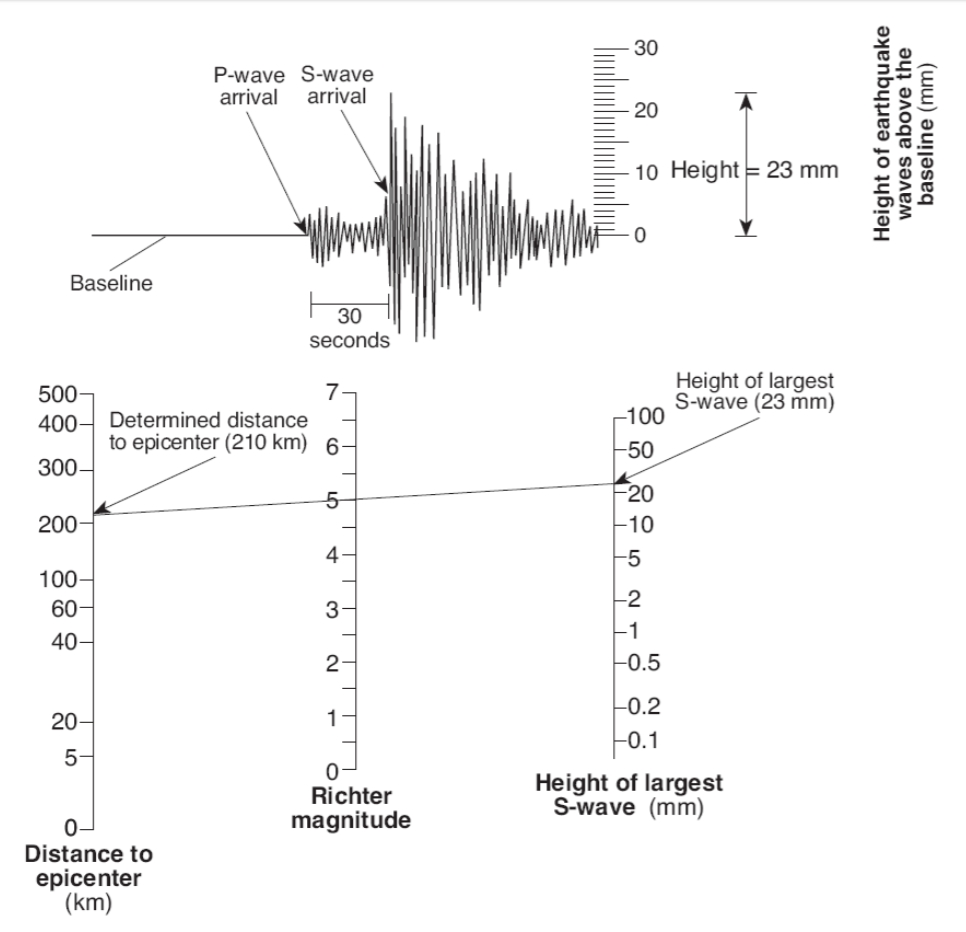
Figure 22. An analog diagram for calculating a Richter scale number for a local earthquake (see http://www.ntschools.org/cms/lib/NY19000908/Centricity/Domain/112/Richter%20worksheet.pdf).
Though relatively easy to understand and use, the Richter Scale is no longer commonly used because it represents just a fraction of what is going on.
There are also Mb (the body-wave magnitude), Ms (the surface-wave magnitude), and Mw (the moment magnitude). Most of these magnitudes track closely together for magnitudes of M = 2 to M = 5, but diverge for larger and smaller earthquakes. In part this is because some wave-types strongly influence a short-period or broadband seismometer (which are sensitive to higher frequencies) while another wave-types (for example, surface waves) more strongly affect older seismometers designed to optimally measure low-frequency energy in the 1 – 2 Hz range.
For large earthquakes, Mw (Moment Magnitude) is the preferred magnitude, because it more fully represents everything emanating from the earthquake hypocenter. The “moment” Mo is calculated as a product of µ (shear strength of the rocks) times S (the surface area of the fault tear, measured horizontally, times down-dip direction), and d (the displacement – how far did one side of the fault move with respect to the other side). The largest ever recorded earthquake, as mentioned earlier was the Great Chilean (Valdivia) event of May 1960, which had a moment magnitude Mw = 9.5
Confused yet? There is also Me (the energy magnitude – a measure of the potential damage to man-made structures), and Intensity (the measure of surface-shaking damage observed). They are related. Energy release is generally proportional to the shaking amplitude raised to the 3/2 power, so an increase of 1 magnitude corresponds to a release of energy 31.6 times greater than that released by the next lower earthquake magnitude. In other words,
Magnitude 3 = 2 gigajoules
Magnitude 4 = 63 gigajoules
Magnitude 5 = 2,000 gigajoules
Magnitude 6 = 63,000 gigajoules
Magnitude 7 = 2,000,000 gigajoules
What is a joule, you may reasonably ask? Energy is normally expressed in joules while power is expressed in watts. One watt is defined as 1 joule per second. A hundred-watt lightbulb, turned on for just one second, consumes 100 joules of total energy.
Both Intensity and Magnitude depend on many local variables, including surface geometry and the seismic velocities of various underlying rock and sediment units. For example, the 1985 Mexico City earthquake had a surface-wave magnitude Ms of 8.1 However, because of resonant focusing of seismic waves as the partially-dried-up Texcoco Lake basin (that Mexico City was built on) lapped onto bedrock, some buildings on one side of a city boulevard had ground motions 75 times greater than the other side (Moreno-Murillo, 1985; see also http://earthquake.usgs.gov/learn/topics/measure.php ). A friend (Mauricio de la Fuente, then a professor at UNAM, the autonomous university of Mexico) who lived through this event told me that it was amazing to stand in that street and see everything on one side standing, and everything on the other side flattened. Over 8,000 people died, mainly in buildings on that ancient lake side (the Texcoco ancient lake bed).
Intensity is very different, based on the Mercalli scale (see https://en.wikipedia.org/wiki/Mercalli_intensity_scale ). It is a twelve-level scale designed to fit observed damage. The name Mercalli is attached to a scale that Giuseppe Mercalli revised from an earlier Rossi-Forel scale, and which has been further modified multiple times since then (http://pubs.usgs.gov/gip/earthq4/severitygip.html ). On the Modified Mercalli scale, the 1985 Mexico City event scored an intensity level of IX (“Violent”) out of a possible twelve. That’s another way of saying “things could be a lot worse.”
One more thing to think about: seismologists estimate that only 1% to 10% of the energy of any given earthquake is released as seismic waves. Almost all the rest of the energy is released as heat (http://earthquake.usgs.gov/learn/topics/measure.php ). This figures indirectly into models designed to emulate the complex breaking process of a fault tear, because at some points, wall-rocks are literally welded together by the intense heat, forcing complex movements around these focal points (Dieterich, 1978; James Dieterich, personal communication 2016). This is an astonishing understanding that goes a long way towards explaining the difficult-to-model nature of a fault rupture.
Moment magnitudes are calculated by complex equations that take into account a number of factors including different velocities and different attenuation of seismic energy in different rocks. Mw takes into account pretty much everything that goes on during the rupture. If you want the gory details, see https://en.wikipedia.org/wiki/Moment_magnitude_scale .
- The “power of a volcano” is generally characterized as Volcano Explosivity Index or VEI. This is a relative measure of explosiveness of volcanic eruptions, and is open-ended with the largest supervolcano eruptions in pre-history (Yellowstone, Toba, Taupo) given an arbitrary magnitude of 8 in this classification system. The 79 AD eruption of Vesuvius and the 1980 eruption of Mount St Helens in Washington State are both rated a VEI 5 on this scale. The VEI number attached to a volcanic eruption depends on (a) how much volcanic material (dense rock equivalent) is thrown out, (b) to what height is it launched, and (c) how long the eruption lasts. There is no equation to calculate this scale, and in that sense it is like the Meercalli Scale. However, it is considered logarithmic from VEI 2 upwards. In other words, a VEI = 5 event represents approximately 10 times more energy released than a VEI = 4 event. Follow this link for more information on how to assess the VEI magnitude (from Newhall and Self, 1982):
https://en.wikipedia.org/wiki/Volcanic_Explosivity_Index
Chapter References:
Allaby, Michael, 2008, Saffir-Simpson scale, in: A dictionary of earth sciences (3rd ed.): Oxford University Press, 1672 pp. ISBN 978-0-1992-11944
Bormann, Peter; and James W. Dewey, 2014, The new IASPEI standards for determining magnitudes from digital data and their relation to classical magnitudes: http://gfzpublic.gfz-potsdam.de/pubman/item/escidoc:816929:1/component/escidoc:816928/IS_3.3_rev1.pdf doi: 10.2312/GFZ.NMSOP-2_IS_3.3
Dieterich, James H., 1978, Time-dependent friction and the mechanics of stick-slip: Pure and Applied Geophysics 116, issue 4, p. 790–806. doi: 10.1007/BF00876539
Fujita, Tetsuya Theodore, 1971, Proposed Characterization of Tornadoes and Hurricanes by Area and Intensity: Satellite and Mesometeorology Research Paper 91. Chicago, IL: Department of Geophysical Sciences, University of Chicago.
Moreno-Murillo, Juan Manuel, 1995, The 1985 Mexico Earthquake: Geofisica Colombiana. Universidad Nacional de Colombia 3, p. 5–19. ISSN 0121-2974.
Newhall, Christopher G.; and Self, Stephen, 1982, The Volcanic Explosivity Index (VEI): An Estimate of Explosive Magnitude for Historical Volcanism (PDF): Journal of Geophysical Research 87 (C2), p. 1231–1238. doi: 10.1029/JC087iC02p01231.
Richter, C.F., 1935, An instrumental earthquake magnitude scale (PDF): Bulletin of the Seismological Society of America. Seismological Society of America 25 (1-2), p. 1–32.
Spence, William; Stuart A. Sipkin; and George L. Choy, 1989, Measuring the size of an earthquake, in: Earthquakes and Volcanoes 21, Number 1, 1989. http://earthquake.usgs.gov/learn/topics/measure.php
